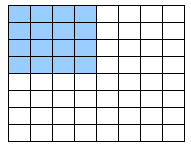
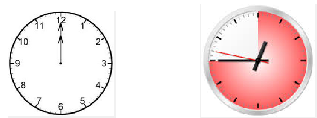
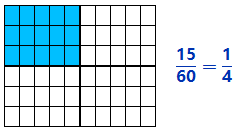
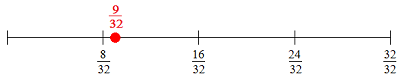Example 1.1.1.
-
\({\dfrac{1}{2}}\) of a dozen eggs (12 eggs) \(=\) 6 eggs\(~~~~~~~~~~~~~~~~~~\blert{\text{A whole dozen is 12 eggs.}~~~~~~~~~~~~\text{Our part is 6 eggs:} ~~\dfrac{6}{12}}\)
 \begin{equation*} \frac{\text{part}}{\text{whole}} = \large{\dfrac{6}{12}} = \large{\dfrac{1}{2}}~~~~~~~~~~~~~~~ \end{equation*}
\begin{equation*} \frac{\text{part}}{\text{whole}} = \large{\dfrac{6}{12}} = \large{\dfrac{1}{2}}~~~~~~~~~~~~~~~ \end{equation*} -
\({\dfrac{1}{2}}\) of an hour (60 minutes) \(=\) 30 minutes\(~~~~~~~~~~~~~~~~~~\blert{\text{A whole hour is 60 minutes.}~~~~~~~~~~\text{Our part is 30 minutes:} ~~\dfrac{30}{60}}\)
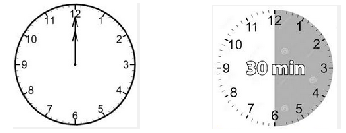 \begin{equation*} \frac{\text{part}}{\text{whole}} = \large{\dfrac{30}{60}} = \large{\dfrac{1}{2}}~~~~~~~~~~~~~~~ \end{equation*}
\begin{equation*} \frac{\text{part}}{\text{whole}} = \large{\dfrac{30}{60}} = \large{\dfrac{1}{2}}~~~~~~~~~~~~~~~ \end{equation*}