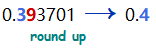Note 2.1.1.
Notice two properties of the metric system:
- Each larger unit is 10, 100 or 1000 times a smaller one.
- The names of related units all use "kilo," "centi," or "milli."
Section 2.1 Decimal Numbers
- Place Value
- Comparing Decimal Fractions
- Fractions to Decimals
- Rounding and Estimating
Subsection 2.1.1 The Metric System
Let’s compare the imperial (everyday, American) system of units with the metric system.
| Imperial System | Metric System |
|---|---|
| \(\blert{\large{\text{Length}}}\) | |
| 1 mile = 1760 yards | 1 kilometer = 1000 meters |
| 1 yard = 3 feet | 1 meter = 100 centimeters |
| 1 foot = 12 inches | 1 centimeter = 10 millimeters |
| \(\blert{\large{\text{Weight}}}\) | |
| 1 ton = 2000 pounds | 1 kilogram = 1000 grams |
| 1 pound = 16 ounces | 1 gram = 100 centigrams |
| 1 ounce = 437.5 grams | 1 centigram = 10 milligrams |
| \(\blert{\large{\text{Volume}}}\) | |
| 1 gallon = 4 quarts | 1 liter = 100 centiliters |
| 1 quart = 2 pints | 1 centiliter = 100 milliliters |
For example, the basic unit of length in the metric system is the meter. Smaller units of length are always one-tenth as long as the previous one.
\begin{align*}
1 ~\text{decimeter} \amp = 0.1 ~\text{meter}\\
1 ~\text{centimeter} \amp = 0.1 ~\text{decimeter} = 0.01 ~\text{meter}\\
1 ~\text{millimeter} \amp = 0.1 ~\text{centimeter} = 0.01 ~\text{decimeter} = 0.001 ~\text{meter}
\end{align*}
The picture below shows a portion of a meter stick. 
The metric system is easy to use because it fits with our base-10 number system. In the same way, decimal fractions are easy to use.
Subsection 2.1.2 Place Value
Remember the place values in our base-10 number system. For example, 
The places after the decimal point represent fractions of a whole number, and it is important to remember that:
Decimal Fractions.
\(\blert{\text{The position of the last digit tells us the denominator of the fraction.}}\)
Activity 2.1.1. Place Value.
Complete the table.
| Decimal Fraction | Common Fraction | Words |
|---|---|---|
| \(0.04\) | \(\dfrac{4}{100}\) | four hundredths |
| \(0.8\) | \(\vphantom{\dfrac{4}{100}}\) | |
| \(\dfrac{7}{1000}\) | ||
| \(\vphantom{\dfrac{4}{100}}\) | one thousandth | |
| \(\dfrac{9}{10}\) | ||
| \(0.002\) | \(\vphantom{\dfrac{4}{100}}\) | |
| \(\vphantom{\dfrac{4}{100}}\) | eight hundredths | |
| \(\dfrac{5}{100}\) | ||
| \(0.03\) | \(\vphantom{\dfrac{4}{100}}\) |
Note 2.1.2.
Be careful when reading decimal fractions! Remember that the position or place value of a digit tells us the denominator of the fraction.
\begin{align*}
0.4~~~~~~ \amp \text{is four tenths} \amp\amp \text{or}~~~~~\dfrac{4}{10}\\
0.04~~~~~~ \amp \text{is four hundredths} \amp\amp \text{or}~~~~~\dfrac{4}{100}\\
0.004~~~~~~ \amp \text{is four thousandths} \amp\amp \text{or}~~~~~\dfrac{4}{1000}
\end{align*}
In the same way, 4 and 40 and 400 are very different numbers.
Here is a way to think of decimal fractions. Imagine that the 10 by 10 by 10 block shown below represents one whole. 
Then one horizontal slice of the block (a "flat") represents one tenth of one whole. One row of the flat (a "stick") represents one hundredth, and one small cube represents one thousandth. 
There are ten flats in a whole, ten sticks in a flat, and ten cubes in a stick. Or, in other words, a flat is one tenth of a whole, a stick is one tenth of a flat, and a cube is one tenth of a stick.
Decimal Places.
\(\blert{\text{Each decimal place is one tenth of the preceding place.}}\)
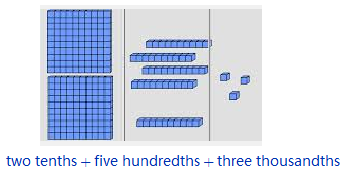
Example 2.1.3.
Use blocks to represent the decimal fraction 0.253 as part of one whole.
Solution.
We read the fraction as "two hundred fifty-three thousandths." (Note that the last digit, 3, is in the thousandths place.)
We can analyze the fraction as follows:
\begin{align*}
0.253~~~~ = ~~~~ 0.2 ~~~~ \amp + ~~~~ 0.05 ~~~~ + ~~~~ 0.003\\
\text{two-tenths} \amp + \text{five-hundredths + three-thousandths}
\end{align*}
Here is the picture of the fraction.
You can check that there are 253 small cubes (thousandths) total.
Checkpoint 2.1.4.
What decimal fraction does this picture represent? 
Answer.
0.636
Subsection 2.1.3 Comparing Decimal Fractions
A study published in the "Journal of the American Medical Association" found that "calculation and decimal point errors accounted for approximately 15% of all prescribing errors in a tertiary care teaching hospital" and "for almost 70% of all detected medication prescribing errors among children."
Everyone should understand how decimal fractions represent portions of a whole.
Example 2.1.5.
Write these decimal fractions in order of size, from smallest to largest.
\begin{equation*}
~~~~0.4,~~~~~~0.36,~~~~~~0.325,~~~~~~0.058
\end{equation*}
Solution.
We’ll look at the place values in each fraction.
\begin{align*}
0.4~~~~\amp 4~ \text{tenths}\\
0.36~~~~\amp 3~ \text{tenths} + 6~ \text{hundredths}\\
0.325~~~~\amp 3~ \text{tenths}+ 2~ \text{hundredths} + 5~ \text{thousandths}\\
0.058~~~~\amp 0~ \text{tenths}+ 5~ \text{hundredths} + 8~ \text{thousandths}
\end{align*}
It might be helpful to picture each fraction using blocks, as demonstrated in Example 1.
We first look at the tenths place; a fraction with more tenths is larger than a fraction with fewer tenths. Thus, 0.4 is the largest fraction in this group, and 0.058 is the smallest.
Next we consider the hundredths place to see that 0.36 is larger than 0.325, because 6 hundredths is larger than 2 hundredths. Thus, the correct order from smallest to largest is
\begin{equation*}
~~~~0.058,~~~~~~0.325,~~~~~~0.36,~~~~~~0.04
\end{equation*}
Here are the four fractions shown on a number line.
Note 2.1.6.
Do not make the \(\alert{\text{ERROR}}\) of thinking that 0.325 is larger than 0.36 because 325 is larger than 36! Remember to compare decimal fractions one decimal place at a time: tenths, then hundredths, etc.
Checkpoint 2.1.7.
Plot the fractions on the number line.
\begin{equation*}
~~~~0.68,~~~~~~0.800,~~~~~~0.92,~~~~~~0.356,~~~~~~0.608
\end{equation*}
Answer.
Note 2.1.8.
Another common \(\alert{\text{ERROR}}\) is to think that 0.058 is larger than 0.4, because "zero doesn’t count." But in this case the zero tells us that
\begin{equation*}
0.\alert{0}58~~~~~~\text{has}~~~~~~\alert{0}~\text{tenths}
\end{equation*}
while
\begin{equation*}
0.\alert{4}~~~~~~\text{has}~~~~~~\alert{4}~\text{tenths}
\end{equation*}
Once again, we compare decimal fractions by comparing each place value in order.
A Quick Fractions Refresher.
There is more than one way to write any particular fraction. For example, the following fractions are all equivalent to \(\dfrac{1}{2}\text{:}\)
\begin{equation*}
\dfrac{2}{4},~~~~~~\dfrac{3}{2},~~~~~~\dfrac{5}{10},~~~~~~\dfrac{25}{50}
\end{equation*}
because each reduces to \(\dfrac{1}{2}\text{.}\)
\(\blert{\text{Exercise:}}\) Write three fractions equivalent to \(\dfrac{2}{3}\text{.}\)
Similarly, there is more than one way to write any particular decimal fraction. The following decimal fractions are equivalent: 
and so on. Each of these fractions reduces to \(\dfrac{7}{10}\text{,}\) or 0.7. Note that the denominator of each decimal fraction is given by the place value of the last digit after the decimal point.
Example 2.1.9.
- Write each decimal fraction as a common fraction.\begin{equation*} ~~~~0.30,~~~~~~0.03,~~~~~~0.030,~~~~~~0.300,~~~~~~0.003 \end{equation*}
- Which fractions are equal?
Solution.
- The denominator of each fraction is given by the place value of the last digit after the decimal point.\begin{align*} 0.30 = \dfrac{30}{100}~~~~~~\amp \text{reduces to}~~\dfrac{3}{10}\\ 0.03 = \dfrac{3}{100}~~~~~~\amp \text{cannot be reduced}\\ 0.030 = \dfrac{30}{1000}~~~~~~\amp \text{reduces to}~~\dfrac{3}{100}\\ 0.300 = \dfrac{300}{1000}~~~~~~\amp \text{reduces to}~~\dfrac{3}{10}\\ 0.003 = \dfrac{3}{1000}~~~~~~\amp \text{cannot be reduced} \end{align*}
- The fractions 0.30 and 0.300 are both equal to \(\dfrac{3}{10}\text{.}\) The fractions 0.03 and 0.030 are both equal to \(\dfrac{3}{100}\text{.}\) We see that an extra zero at the end of a decimal fraction does not change its value.
Checkpoint 2.1.10.
Explain why 0.15 and 0.150 are equivalent fractions, but 0.150 and 0.015 are not equivalent.
\begin{gather*}
0.15 = ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
0.150 = ~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\
0.015 = ~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\end{gather*}
Answer.
\(0.15 = \dfrac{15}{100}\text{,}\) and \(0.150 = \dfrac{150}{1000}\text{,}\) which can be reduced to \(\dfrac{15}{100}\text{,}\) so those two fractions are equal. (Both are equivalent to \(\dfrac{3}{20}\text{.}\)) But \(0.015 = \dfrac{15}{1000} = \dfrac{3}{200}\text{.}\)
Subsection 2.1.4 Fractions to Decimals
Another way to get a feel for decimal fractions is to relate them to familiar common fractions. Remember that the fraction bar is actually a division symbol, so the fraction \(\dfrac{1}{2}\) means "1 divided by 2." If you use your calculator to carry out the division, you will find
\begin{equation*}
\dfrac{1}{2} = 1 \div 2 = 0.5
\end{equation*}
Some decimal equivalents of common fractions terminate or end, like
\begin{equation*}
\dfrac{3}{8} = 0.375
\end{equation*}
but others repeat a pattern of digits without ending, like
\begin{equation*}
\dfrac{5}{6} = 0.833333 ...
\end{equation*}
We denote these repeating decimals with a bar over the digits that repeat, like this:
\begin{equation*}
\dfrac{5}{6} = 0.8\overline{3}
\end{equation*}
Example 2.1.11.
Write the decimal equivalent of the fraction \(\dfrac{3}{11}\text{.}\)
Solution.
We use a calculator to compute \(3 \div 11\)
\begin{equation*}
\dfrac{3}{11} = 3 \div 11 = 0.27272727 ...
\end{equation*}
We write the result with a repeater bar: \(\dfrac{3}{11} = 0.\overline{27}\text{.}\)
Checkpoint 2.1.12.
Write the decimal equivalent of the fraction \(\dfrac{7}{22}\text{.}\)
Answer.
\(0.3\overline{18}\)
Activity 2.1.2. Decimal Equivalents.
-
Use your calculator to find the decimal equivalent of each common fraction. Use a repeater bar to denote any repeating decimals.
Fraction Decimal Fraction Decimal \(\dfrac{1}{3}\) \(\hphantom{000000}\) \(\dfrac{4}{5}\) \(\hphantom{000000}\) \(\dfrac{2}{3}\) \(\hphantom{000000}\) \(\dfrac{1}{6}\) \(\hphantom{000000}\) \(\dfrac{1}{4}\) \(\hphantom{000000}\) \(\dfrac{5}{6}\) \(\hphantom{000000}\) \(\dfrac{3}{4}\) \(\hphantom{000000}\) \(\dfrac{1}{8}\) \(\hphantom{000000}\) \(\dfrac{1}{5}\) \(\hphantom{000000}\) \(\dfrac{3}{8}\) \(\hphantom{000000}\) \(\dfrac{2}{5}\) \(\hphantom{000000}\) \(\dfrac{5}{8}\) \(\hphantom{000000}\) \(\dfrac{3}{5}\) \(\hphantom{000000}\) \(\dfrac{7}{8}\) \(\hphantom{000000}\) -
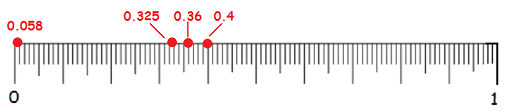
Plot each decimal fraction on the number line below.
- Which of the fractions above are repeating decimals?
Question.
Is there a way to tell which fractions have terminating decimals, and which ones have repeating decimals?
Subsection 2.1.5 Rounding and Estimating
My town has a population of 8300 people. Is that closer to 8000 people or 9000 people? If we count by 100’s, 8300 is closer to 8000.
So if I round the population to 1000’s of people, my town’s population is about 8000. In fact, we can say that any population less than 8500 is about 8000, and a population 8500 or above is about 9000.
Example 2.1.13.
Is 0.837 closer to 0.8 or to 0.9?
Solution.
In this Example, we are rounding to the nearest tenth. We use the same reasoning as above: because 3 is less than 5, 0.8\(\blert{3}\)7 is closer to 0.8.
Note 2.1.14.
In the last example, we rounded down to the nearest tenth. To decide which way to round, we looked at the next digit, in the hundredths place, to see if it was greater than or less than 5. We did not have to consider the 7 in the thousandths place -- it is too small to make a difference in this case.
We can round a number to any place-value we like. In the next Exercise, we round to the hundredths place.
Checkpoint 2.1.15.
Round 0.258 to hundredths. (Is 0.258 closer to 0.25 or to 0.26?) Illustrate on the number line.
Answer.
\(0.26\)
Activity 2.1.3. Rounding.
Fill in the blanks.
- When we round to the nearest tenth, we look at the digit in the place. If that digit is less than , we round to the smaller tenth. If that digit is or greater, we round up to the larger tenth.
- When we round to the nearest hundredth, we look at the digit in the place. If that digit is less than , we round to the smaller hundredth. If that digit is or greater, we round up to the larger hundredth.
- When we round to any place value, we look at the digit to the of that place. If that digit is less than , we . If that digit is or greater, we .
Example 2.1.16.
Find the decimal form of each fraction. Round your answers to hundredths.
- \(\displaystyle \dfrac{3}{7}\)
- \(\displaystyle \dfrac{2}{7}\)
Solution.
- We use a calculator to divide 3 by 7.\begin{equation*} \dfrac{3}{7} = 3 \div 7 = 0.428571 ...~~~~~~~~~\blert{\text{2 is in the hundredths place.}} \end{equation*}To round to hundredths, we look at the digit after the hundredths place, which in this case is 8. If that digit is 5 or more, we round up to the next hundredth, to get 0.43. So, \(\dfrac{3}{7}\) is approximately 0.43.
- We use a calculator to divide 5 by 7.\begin{equation*} \dfrac{5}{7} = 5 \div 7 = 0.714285 ...~~~~~~~~~\blert{\text{1 is in the hundredths place.}} \end{equation*}The digit after the hundredths place is 4, which is less than 5, so we round down to 0.71. So, \(\dfrac{5}{7}\) is approximately 0.71.
To understand rounding, we need to think about place value. In Example 6(a), the number \(0.4\blert{28}\) is between \(0.4\blert{20}\) and \(0.4\blert{30}\text{,}\) but it is closer to 0.430, just as 28 is closer to 30 than it is to 20. So we round up to 0.430, or just 0.43.
In part (b), the number \(0.7\blert{14}\) is between \(0.7\blert{10}\) and \(0.7\blert{20}\text{,}\) but it is closer to 0.710, just as 14 is closer to 10 than it is to 20. So we round down to 0.710, or just 0.71.
Note 2.1.17.
In Example 6, it is important to realize that \(\dfrac{3}{7}\) is \(\alert{\text{not equal}}\) to 0.43; it is only \(\alert{\text{approximately equal}}\) to 0.43. Whenever we round off a decimal fraction, the result is always an approximation.
Checkpoint 2.1.18.
Write the decimal form of each fraction. Round to hundredths if the decimal does not terminate. Is this decimal form exactly equal to the fraction, or an approximation?
| Fraction | Decimal Form | Equal (Yes or No) |
|---|---|---|
| \(\dfrac{3}{5}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\dfrac{7}{20}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\dfrac{1}{3}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\dfrac{4}{9}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\dfrac{8}{25}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\dfrac{2}{3}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
Answer.
| Fraction | Decimal Form | Equal (Yes or No) |
|---|---|---|
| \(\dfrac{3}{5}\) | \(0.6\) | Yes |
| \(\dfrac{7}{20}\) | \(0.35\) | Yes |
| \(\dfrac{1}{3}\) | \(0.33\) | No |
| \(\dfrac{4}{9}\) | \(0.44\) | No |
| \(\dfrac{8}{25}\) | \(0.32\) | Yes |
| \(\dfrac{2}{3}\) | \(0.67\) | No |
Example 2.1.19.
How big is one centimeter? A centimeter is 0.393701 of one inch. Round this fraction to the nearest tenth, and compare it to the decimal equivalents of common fractions in Activity 2.
Solution.
To round to tenths we look at the digit in the hundredths place. Because 9 is greater than 5, we round up to 0.4.
A centimeter is approximately 0.4 of one inch. By consulting Activity 2, we see that 0.4 is equal to \(\dfrac{2}{5}\text{.}\) (Or we can reduce \(\dfrac{4}{10}\) to \(\dfrac{2}{5}\text{.}\)) So one centimeter is a little smaller than \(\dfrac{2}{5}\) of an inch.
Checkpoint 2.1.20.
- One kilometer is 0.621371 of one mile. How many miles long is a 10K (10 kilometer) race?
- Round your answer to part (a) to tenths, and compare to the closest familiar common fraction.
Answer.
- 6.21371 miles
- Approximately 6.2 miles, or \(6\dfrac{1}{5}\) miles
Subsection 2.1.6 Vocabulary
- metric system
- meter
- decimal fraction
- place value
- terminate
- repeating decimal
- rounding
Exercises 2.1.7 Practice 2.1
Exercise Group.
For Problems 1-8,
- Write the decimal fraction as a common fraction.
- Write the name of the fraction in words.
1.
\(0.8\)
2.
\(0.5\)
3.
\(0.009\)
4.
\(0.002\)
5.
\(0.07\)
6.
\(0.04\)
7.
\(0.0003\)
8.
\(0.0006\)
Exercise Group.
For Problems 9-16,
- Write the decimal fraction as a common fraction.
- Write the name of the fraction in words.
9.
\(0.28\)
10.
\(0.39\)
11.
\(0.452\)
12.
\(0.618\)
13.
\(0.064\)
14.
\(0.098\)
15.
\(0.050\)
16.
\(0.800\)
Exercise Group.
For Problems 17-24,
- Represent the fraction with flats, sticks, and cubes.
- Write the fraction as a sum of tenths, hundredths, and thousandths.
17.
\(0.317\)
18.
\(0.425\)
19.
\(0.034\)
20.
\(0.016\)
21.
\(0.102\)
22.
\(0.203\)
23.
\(0.430\)
24.
\(0.020\)
Exercise Group.
In Problems 25-28, each 10 by 10 grid represents one whole. Shade the fraction of the grid.
25.
-
\(\displaystyle 0.3\)
-
\(\displaystyle 0.03\)
-
\(\displaystyle 0.33\)
26.
-
\(\displaystyle 0.15\)
-
\(\displaystyle 0.05\)
-
\(\displaystyle 0.005\)
27.
-
\(\displaystyle \dfrac{1}{4}\)
-
\(\displaystyle \dfrac{1}{8}\)
-
\(\displaystyle \dfrac{1}{5}\)
28.
-
\(\displaystyle \dfrac{2}{5}\)
-
\(\displaystyle \dfrac{5}{8}\)
-
\(\displaystyle \dfrac{3}{20}\)
Exercise Group.
For Problems 29-36, round the fraction to hundredths and plot the result on the number line.
29.
\(0.5283\)
30.
\(0.3649\)
31.
\(0.6666\)
32.
\(0.2222\)
33.
\(0.8994\)
34.
\(0.4950\)
35.
\(0.1386\)
36.
\(0.0097\)
Exercise Group.
For Problems 37-40,
- Write the fractions in order from smallest to largest.
- Label the number line with appropriate values and plot the fractions.
37.
\(0.46,~0.5,~0.200,~0.08\)
38.
\(1.06,~1.6,~1.66,~1.16\)
39.
\(0.34,~0.36,~0.316,~0.304\)
40.
\(0.015,~0.051,~0.02,~0.1\)
Exercise Group.
For Problems 41-42, complete the table with equivalent expressions, as shown in the example below.
| Units | Tenths | Hundredths | Thousandths |
|---|---|---|---|
| \(3.2\) | \(32\) | \(320\) | \(3200\) |
41.
| Units | Tenths | Hundredths | Thousandths |
|---|---|---|---|
| \(8.56\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\hphantom{000000}\) | \(45\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\hphantom{000000}\) | \(\hphantom{000000}\) | \(7\) | \(\hphantom{000000}\) |
42.
| Units | Tenths | Hundredths | Thousandths |
|---|---|---|---|
| \(2.05\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\hphantom{000000}\) | \(6.2\) | \(\hphantom{000000}\) | \(\hphantom{000000}\) |
| \(\hphantom{000000}\) | \(\hphantom{000000}\) | \(5.9\) | \(\hphantom{000000}\) |
Exercise Group.
For Problems 43-50, write the decimal form of each fraction, rounded to hundredths if necessary. Is this decimal form exactly equal to the fraction, or an approximation?
43.
\(\dfrac{13}{20}\)
44.
\(\dfrac{5}{8}\)
45.
\(\dfrac{5}{6}\)
46.
\(\dfrac{8}{9}\)
47.
\(\dfrac{17}{25}\)
48.
\(\dfrac{39}{50}\)
49.
\(\dfrac{4}{7}\)
50.
\(\dfrac{3}{11}\)
Exercise Group.
For Problems 51-58, replace the decimal fraction with one of the familiar common fractions from Activity 2.1.2, so that you can say: "This number is approximately equal to \(\fillinmath{XXX}\text{.}\)"
51.
\(2.8025\)
52.
\(6.3851\)
53.
\(3.673\)
54.
\(7.739\)
55.
\(0.124\)
56.
\(1.626\)
57.
\(4.334\)
58.
\(5.498\)
Exercise Group.
For Problems 59-62, use only your knowledge of place value and the result of the calculation shown to find the products.
59.
\(24 \times 65 = 1560\)
- \(\displaystyle 2.4 \times 65\)
- \(\displaystyle 0.24 \times 65\)
- \(\displaystyle 2.4 \times 6.5\)
- \(\displaystyle 0.24 \times 0.65\)
60.
\(33 \times 89 = 2937\)
- \(\displaystyle 0.33 \times 89\)
- \(\displaystyle 3.3 \times 8.9\)
- \(\displaystyle 3.3 \times 0.89\)
- \(\displaystyle 33 \times 8.9\)
61.
\(41 \times 52 = 2132\)
- \(\displaystyle 4.1 \times 5.2\)
- \(\displaystyle 0.41 \times 52\)
- \(\displaystyle 0.41 \times 0.52\)
- \(\displaystyle 41 \times 520\)
62.
\(88 \times 73 = 6424\)
- \(\displaystyle 8.8 \times 73\)
- \(\displaystyle 0.88 \times 73\)
- \(\displaystyle 0.88 \times 7.3\)
- \(\displaystyle 88 \times 0.73\)
63.
What does it mean for a decimal fraction to terminate?
64.
How do we denote a repeating decimal fraction?
65.
Is \(0.3\) equal to \(0.\overline{3}\) ? Explain why or why not.
66.
- Explain the dfference between \(0.\overline{25}\) and \(0.2\overline{5}\text{.}\)
- Find the decimal equivalents of \(\dfrac{25}{99}\) and \(\dfrac{23}{90}\text{.}\)
67.
- Is there a decimal fraction between 1.9 and 2?
- Is there a decimal fraction between 1.99 and 2?
- Is there a decimal fraction between 1.999 and 2?
- Describe a way to find a decimal fraction between any two numbers.
68.
What familiar number is equal to 0.9999… ?
