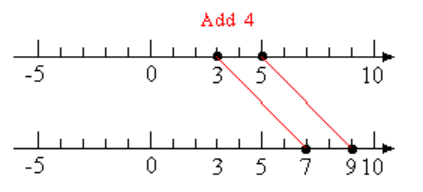
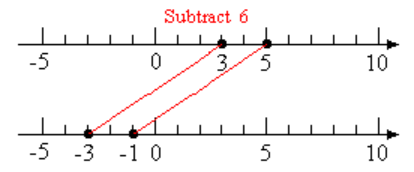
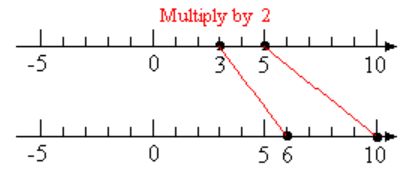
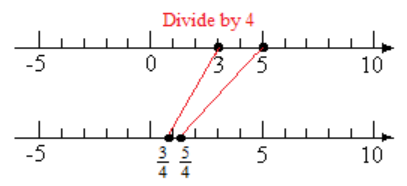
Example 2.50.
The equation
\begin{equation*}
T=50+15u
\end{equation*}
describes college tuition consisting of a $50 registration fee plus $15 per unit. How many units can you take if you have $290 saved for tuition?
Solution.
We can answer the question by solving the equation
\begin{equation*}
\alert{290}=50+15u
\end{equation*}
where we have substituted $290 for the tuition, \(T\text{.}\) Think about the expression \(50+15u\text{.}\) How would you evaluate this expression if you were given a value for \(u\text{?}\) Following the order of operations, you would
\begin{align*}
\amp 1.~~~\text{First multiply by 15}\\
\amp 2.~~~\text{Then add 50}
\end{align*}
In order to solve the equation, we must reverse these two steps to undo the operations and isolate the variable. We first subtract 50 from both sides of the equation:
\begin{align*}
290 ~\amp = ~~~50+15u \amp \amp \blert{\text{Subtract 50 from both sides.}}\\
\underline{\blert{-50}} \amp = \underline{\blert{-50}}\\
240 ~\amp = ~~~~~~~~~~~~~15u
\end{align*}
This isolates the term that contains the variable, \(15u\text{.}\) Then we divide both sides of the equation by 15.
\begin{equation*}
\begin{aligned}
\dfrac{240}{\blert{15}} \amp = \dfrac{15u}{\blert{15}} \amp \amp \blert{\text{Divide both sides by 15.}}\\
16 \amp = u
\end{aligned}
\end{equation*}
You can enroll in 16 units. We can check the solution by substituting 16 for \(u\) in the original equation.
\begin{align*}
\blert{\text{Check:}}~~~~~~~~~~~~ 50+15u =\amp 290\\
50+15(\alert{16}) =\amp 50+240=290 ~~~~~ \blert{\text{True}}
\end{align*}
Because a true statement results, the solution checks.