Subsection The Natural Exponential Function
The natural exponential function is the function
\begin{equation*}
f(x) = e^x
\end{equation*}
Values for \(e^x\) can be obtained with a calculator using the \(\boxed{e^x}\) key ( 2nd LN on most calculators). For example, you can evaluate \(e^1\) by pressing
2nd LN \(1\)
to confirm the value of \(e\) given above. (We’ll explain why we use the 2nd LN key a little later.)
Try a few more calculations to become familiar with base \(e\text{.}\)
Checkpoint 5.61. Practice 1.
Use your calculator to evaluate the following powers. Round to four decimal places.
\(\displaystyle e^2\)
\(\displaystyle e^{3.5}\)
\(\displaystyle e^{-0.5}\)
Solution.
\(\displaystyle e^2\approx 7.3891\)
\(\displaystyle e^{3.5}\approx 33.1155 \)
\(\displaystyle e^{-0.5}\approx 0.6065 \)
What about the graph of this new exponential function? Because \(e\) is a number between \(2\) and \(3\text{,}\) the graph of \(f(x) = e^x\) lies between the graphs of \(y = 2^x\) and \(y = 3^x\text{.}\) Compare the tables of values and the graphs of the three functions below. For example, note that for \(x=2\text{,}\) the value of \(e^2 = 7.389\) is between \(2^2 = 4\) and \(3^2 = 9\text{.}\) You can verify the table and graphs on your calculator.
| \(x\) |
\(y=2^x\) |
\(y=e^x\) |
\(y=3^x\) |
| \(-3\) |
\(0.125\) |
\(0.050\) |
\(0.037\) |
| \(-2\) |
\(0.250\) |
\(0.135\) |
\(0.111\) |
| \(-1\) |
\(0.500\) |
\(0.368\) |
\(0.333\) |
| \(0\) |
\(1\) |
\(1\) |
\(1\) |
| \(1\) |
\(2\) |
\(2.718\) |
\(3\) |
| \(2\) |
\(4\) |
\(7.389\) |
\(9\) |
| \(3\) |
\(8\) |
\(20.086\) |
\(27\) |
Checkpoint 5.62. QuickCheck 1.
-
The value of \(e^2\) is closest to which of these?
\(\displaystyle 3\)
\(\displaystyle 5\)
\(\displaystyle 7\)
\(\displaystyle 9\)
-
The value of \(e^{-1}\) is closest to which of these?
\(\displaystyle -3\)
\(\displaystyle \dfrac{1}{2}\)
\(\displaystyle \dfrac{1}{3}\)
\(\displaystyle 2\)
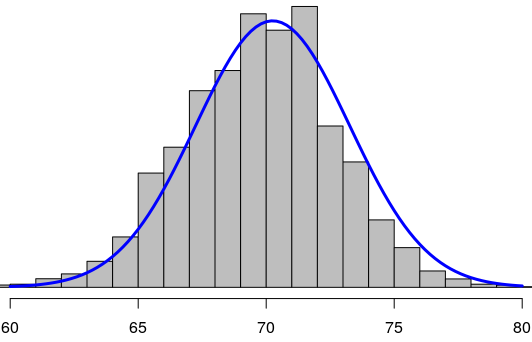
Variations on the natural exponential function occur in many disciplines. For example, the graph in the figure below is called a "bell curve." It is the graph of the normal distribution in statistics.
Example 5.63.
The normal distribution above shows the heights of men in the US. The average or mean height for men is 70 inches, and the formula for the graph is
\begin{equation*}
f(x) = 0.13~ e^{-(x-70)^2/18}
\end{equation*}
The probability that a given man has a height between two values is the area under the curve between those values. Evaluate the function for \(x=70\) and for \(x=67\text{.}\)
Solution.
To evaluate the function we follow the order of operations. For \(x=70\) we have
\begin{align*}
f(70) \amp = 0.13~ e^{-(70-70)^2/18} \amp \amp \blert{\text{Simplify the exponent first.}}\\
\amp = 0.13~ e^0 = 0.13
\end{align*}
For \(x=67\) we have
\begin{align*}
f(67) \amp = 0.13~ e^{-(67-70)^2/18} \amp \amp \blert{-(67-70)^2/18 = -0.5} \\
\amp = 0.13~ e^{-0.5} = 0.079
\end{align*}
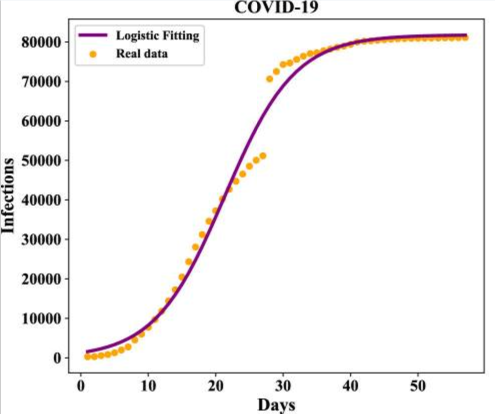
This next graph is an example of a logistic function, which models population growth with an upper bound.
Checkpoint 5.64. Practice 2.
The logistic function shown above models the spread of Covid in China during the 2020 epidemic. It gives the number of infections \(N(t)\text{,}\) in thousands, reported \(t\) days after January 21, 2020. The equation for this model is
\begin{equation*}
N(t) = \dfrac{83.5}{1+267~ e^{-0.214t}}
\end{equation*}
According to the model, how many cases of Covid were reported on February 20 (day \(t=30\))?
Example 5.65.
Use technology to graph each function. How does each graph differ from the graph of \(y = e^x\text{?}\)
\(\displaystyle g(x) = e^{x+2}\)
\(\displaystyle h(x) = e^x + 2\)
Solution.
The graph of \(g\) is shifted \(2\) units to the left of \(y = e^x\text{.}\) The graph of \(h\) is shifted \(2\) units up from \(y = e^x\text{.}\) The graphs are shown above.
Subsection The Natural Logarithmic Function
Recall that each exponential function with base \(b\) has an inverse function, the logarithmic function with the same base. For example, the function \(~y=\log_2{(x)}~\) is the inverse of the function \(~y=2^x\text{.}\) It gives the exponent needed on 2 to give \(x\text{,}\) so that, for instance, \(~\log_2{(16)} = 4~\text{,}\) because \(~2^4 = 16\text{.}\)
The base \(e\) logarithm of a number \(x\text{,}\) or \(\log_ e x\text{,}\) is called the natural logarithm of \(x\) and is denoted by \(\ln x\text{.}\) (Why “ln” and not “nl”? The natural logarithm is denoted by “ln” because it stands for “logarithmus naturalis,” which is the Latin for “natural logarithm.”) Here is its official definition.
The Natural Logarithm.
The natural logarithm is the logarithm base \(e\text{.}\)
\begin{equation*}
\ln x = \log_{e}{x}, ~~~~ x\gt 0
\end{equation*}
The natural logarithm of \(x\) is the exponent to which \(e\) must be raised to produce \(x\text{.}\) For example, the natural logarithm of \(10\text{,}\) or \(\ln 10\text{,}\) is the solution of the equation
\begin{equation*}
e^y = 10
\end{equation*}
You can verify on your calculator that
\begin{equation*}
e^{\alert{2.3}} ~~ \approx 10 \text{ or } ~~ \ln 10 \approx \alert{2.3}
\end{equation*}
As is the case with exponential and log functions with other bases, the natural log function, \(y= \ln {(x)}\text{,}\) and the natural exponential function, \(f(x) = e^x\text{,}\) “undo” each other, so they are inverse functions. (This is why many calculators use 2nd LN to indicate \(e^x\text{.}\))
Checkpoint 5.66. Practice 3.
Use your calculator to evaluate each logarithm. Round your answers to four decimal places.
\(\displaystyle \ln {(10)}\)
\(\displaystyle \ln {(0.1)}\)
\(\displaystyle \ln {(100)}\)
\(\displaystyle \ln {(0.01)}\)
Solution.
\(\displaystyle \ln {(10)}\approx 2.3026\)
\(\displaystyle \ln {(0.1)}\approx -2.3026\)
\(\displaystyle \ln {(100)}\approx 4.6052\)
\(\displaystyle \ln {(0.01)}\approx -4.6052\)
As usual, we can gain a better understanding of a new function by looking at its graph.
Example 5.67.
Graph \(~f(x) = e^x~\) and \(~g(x) = \ln {(x)}~\) on the same grid.
Give the domain and range of the natural log function.
Solution.
Earlier we made a table of values to graph the fuction \(f(x) = e^x\text{,}\) and we can make a table of values for \(g(x) = \ln {(x)}\) by interchanging the columns in that table. Plotting the points gives us the graph below.
| \(x\) |
\(y=\ln {(x)}\) |
| \(0.050\) |
\(-3\) |
| \(0.135\) |
\(-2\) |
| \(0.368\) |
\(-1\) |
| \(1\) |
\(0\) |
| \(2.718\) |
\(1\) |
| \(7.389\) |
\(2\) |
| \(20.086\) |
\(3\) |
You can see that the graph of \(g(x) = \ln {(x)}\) is the reflection of the graph of \(f(x) = e^x\) about the line \(y=x\text{.}\) In particular, notice that while the graph of \(f(x) = e^x\) has no points with negative \(y\)-values, the graph of \(g(x) = \ln {(x)}\) has no points with negative \(x\)-values. Thus, the domain of the natural log function is the same as the range of \(y = e^x\text{,}\) or all positive numbers. The range of \(y = \ln x\) is the same as the domain of \(y = e^x\text{,}\) or all real numbers.
From the graph of \(g(x) = \ln {(x)}\) you can make the following observations.
The natural log function has only positive numbers as input values.
The natural logs of negative numbers and zero are undefined.
The natural log of a number greater than 1 is positive, while the logs of numbers between 0 and 1 are negative.
Subsection Properties of the Natural Logarithm
Natural logs obey the same conversion formulas that work for logs to other bases.
Conversion Formulas for Natural Logs.
\begin{equation*}
\blert{y = \ln x} ~~\text{ if and only if } ~~ \blert{e^y = x}
\end{equation*}
The conversion formulas are just another way of saying the the the natural log function, \(g(x) = \ln x\text{,}\) and the natural exponential function, \(f(x) = e^x\text{,}\) are inverse functions.
In particular,
\begin{equation*}
\begin{aligned}[t]
\ln e \amp = 1 \text{ because } e^1 = e \\
\ln 1 \amp = 0 \text{ because } e^0 = 1 \\
\end{aligned}
\end{equation*}
Checkpoint 5.68. QuickCheck 2.
Which of the following is equivalent to \(e^x=k\) ?
\(\displaystyle e^k=x\)
\(\displaystyle \ln{(e)} = x\)
\(\displaystyle \ln{(k)} = x\)
\(\displaystyle k^x = e\)
We use natural logarithms in the same way that we use logs to other bases. The properties of logarithms that we studied in
Section 4.4 also apply to logarithms base
\(e\text{.}\)
Properties of Natural Logarithms.
If \(x, y \gt 0\text{,}\) then
\(\displaystyle \ln{(xy)} = \ln{x} + \ln{y}\)
\(\displaystyle \ln\dfrac{x}{y} = \ln x - \ln y\)
\(\displaystyle \ln{x^k} = k \ln x \)
Because the functions \(y = e^x\) and \(y = \ln x\) are inverse functions, the following properties are also true.
The Natural log and \(e^x\).
\begin{equation*}
\ln{e^x} = x,~~\text{ for all }x, ~~~~~\text{ and }~~~e^{\ln x} = x,~~\text{ for }x \gt 0
\end{equation*}
Example 5.69.
Simplify each expression.
\(\displaystyle \ln e^{0.3x}\)
\(\displaystyle e^{2 \ln(x+3)}\)
Solution.
The natural log is the log base \(e\text{,}\) and hence the inverse of \(e^x\text{.}\) Therefore,
\begin{equation*}
\ln {e^{0.3x}} = 0.3x
\end{equation*}
First, we simplify the exponent using the third property of logs to get
\begin{equation*}
2 \ln(x + 3) = \ln(x + 3)^2
\end{equation*}
Then \(e^{2 \ln(x+3)} = e^{\ln(x+3)^2} = (x + 3)^2\text{.}\)
Checkpoint 5.70. Practice 4.
Simplify each expression.
\(\displaystyle e^{(\ln {(x)}/2)}\)
\(\displaystyle \ln{\left(\dfrac{1}{e^{4x}}\right)}\)
Solution.
\(\sqrt{x}~\) or \(~x^{1/2}\)
\(\displaystyle -4x\)
Checkpoint 5.71. Pause and Reflect.
Explain why \(\ln\dfrac{1}{e^3} = -3\text{.}\)
Subsection Solving Equations
We use the natural logarithm to solve exponential equations with base \(e\text{.}\) The techniques we’ve learned for solving other exponential equations also apply to equations with base \(e\text{.}\)
Example 5.72.
Solve each equation for \(x\text{.}\)
\(\displaystyle e^x = 0.24\)
\(\displaystyle \ln x = 3.5\)
Solution.
We convert the equation to logarithmic form and evaluate using a calculator.
\begin{equation*}
x = \ln 0.24 \approx -1.427
\end{equation*}
We convert the equation to exponential form and evaluate.
\begin{equation*}
x = e^{3.5} \approx 33.1155
\end{equation*}
Checkpoint 5.73. Practice 5.
Solve each equation. Round your answers to four decimal places.
\(\displaystyle \ln {(x)} =-0.2\)
\(\displaystyle e^x = 8\)
Solution.
\(\displaystyle 0.8187 \)
\(\displaystyle 2.0794\)
Checkpoint 5.74. QuickCheck 3.
Which statement below explains why the equation \(e^x=6.5\) is easier to solve than \(8^x=6.5\) ?
8 is larger than 6.5.
\(k\) is a constant.
There is a button for log base \(e\) on the calculator, but not a button for log base 8.
Because \(e\) is an irrational number.
To solve more complicated exponential equations, we isolate the power on one side of the equation before converting to logarithmic form.
Example 5.75.
Solve \(~200 = 60 + 20 e^{0.4x}\)
Solution.
First, we isolate the power.
\begin{align*}
200 \amp = 60 + 20 e^{0.4x} \amp \amp \blert{\text{Subtract 60 from both sides.}}\\
140 \amp = 20 e^{0.4x} \amp \amp \blert{\text{Divide both sides by 20.}}\\
7 \amp = e^{0.4x}
\end{align*}
Then we convert the equation to logarithmic form.
\begin{align*}
0.4x \amp = \ln {(7)} \amp\amp \blert{\text{Divide both sides by 0.4.}}\\
x \amp= \frac{\ln {(7)}}{0.4}
\end{align*}
Rounded to four decimal places, \(x \approx 4.8648\text{.}\)
Checkpoint 5.77. Practice 6.
Solve
\begin{equation*}
~80 -16e^{-0.2x} = 70.3
\end{equation*}
Solution.
Isolate the power, take the natural log of both sides, and solve as usual to find \(x = -5 \ln \left(\dfrac{9.7}{16} \right)\approx 2.5023\)
Example 5.78.
The logistic function
\begin{equation*}
P = \dfrac{20}{1 + 5e^{-0.4t}}
\end{equation*}
has its upper bound at \(~P=20\text{.}\) Find the value of \(t\) for which \(~P=10\text{.}\)
Solution.
We must solve the equation \(~10 = \dfrac{20}{1 + 5e^{-0.4t}}~\) for \(t\text{.}\) To begin, we multiply both sides of the equation by the denominator, \(1 + 5e^{-0.4t}\text{,}\) to get
\begin{equation*}
1 + 5e^{-0.4t} = \dfrac{20}{10} = 2
\end{equation*}
Then we isolate the power, \(e^{-kt}\text{,}\) as follows:
\begin{align*}
1 + 5e^{-0.4t} \amp = 2 \amp \amp \blert{\text{Subtract 1 from both sides, then divide by 5.}}\\
e^{-0.4kt} \amp = 0.2
\end{align*}
Next, we take the natural logarithm of both sides to get
\begin{equation*}
\ln {(e^{-0.4t})} = \ln{(0.2)}
\end{equation*}
and recall that \(\ln {(e^x)} = x\) to simplify the left side.
\begin{equation*}
-0.4t = \ln{(0.2)}
\end{equation*}
Finally, we divide both sides by \(-0.4\) to solve for \(t\text{.}\)
\begin{equation*}
t =\frac{-\ln{(0.2)}}{0.4} \approx 4.02
\end{equation*}
Checkpoint 5.79. Practice 7.
Solve \(N = Ae^{-kt}\) for \(k\text{.}\)
Solution.
\(k=\dfrac{-\ln{(N/A)} }{t} \)
Checkpoint 5.80. Pause and Reflect.
Delbert says that he will begin solving the equation \(100e^{0.6t}=40\) by computing \(e^{0.6t}\text{.}\) Is this a good strategy? Why or why not?
Subsection Exponential Growth and Decay
\begin{equation*}
P(t) = P_0\cdot b^t
\end{equation*}
which describe exponential growth when \(b \gt 1\) and exponential decay when \(0 \lt b \lt 1\text{.}\) Exponential growth and decay can also be modeled by functions of the form
\begin{equation*}
\blert{P(t) = P_0 \cdot e^{kt}}
\end{equation*}
where we have substituted \(e^k\) for the growth factor \(b\text{,}\) so that
\begin{equation*}
\begin{aligned}[t]
P(t) \amp = P_0 \cdot b^t\\
\amp = P_0 \cdot \left(e^k\right)^t = P_0 \cdot e^{kt}\\
\end{aligned}
\end{equation*}
We can find the value of \(k\) by solving the equation \(b = e^k\) for \(k\text{,}\) to get \(k = \ln b\text{.}\)
For instance, consider a colony of bacteria grows according to the formula
\begin{equation*}
P(t) = 100 \cdot \alert{3^t}
\end{equation*}
We can express this function in the form \(P(t) = 100 \cdot \alert{e^{kt}}\) if we set
\begin{equation*}
3 = e^k ~ \text{ or } ~ k = \ln 3 \approx 1.0986
\end{equation*}
Thus, the growth law for the colony of bacteria can be written
\begin{equation*}
P(t) \approx 100 \cdot e^{1.0986t}
\end{equation*}
By graphing both functions on your calculator, you can verify that
\begin{gather*}
P(t) = 100 \cdot 3^t\\
~~~\text{and}~~~\\
P(t) = 100 \cdot e^{1.0986t}
\end{gather*}
are just two ways of writing the same function.
Sometimes exponential growth is given as a percentage, so for example we might say “prices rose by 5% annually.” In this case the growth factor is \(~b=1+r~\text{,}\) where \(r\) is the percentage rate in decimal form. For a percent decrease, \(~b=1-r~\text{.}\)
Example 5.81.
From 1990 to 2000, the population of Clark County, Nevada, grew by \(6.4\%\) per year.
What was the growth factor for the population of Clark County from 1990 to 2000? If the population of Clark County was \(768,000\) in 1990, write a formula for the population \(t\) years later.
Write a growth formula for Clark County using base \(e\text{.}\)
Solution.
The growth factor was \(b = 1 + r = 1.064\text{.}\) The population \(t\) years later was
\begin{equation*}
P(t) = 768,000 (1.064)^t
\end{equation*}
We use the formula \(P(t) = P_0 \cdot e^{kt}\text{,}\) where \(e^k = 1.064\text{.}\) Solving for \(k\text{,}\) we find
\begin{equation*}
k = \ln 1.064 = 0.062
\end{equation*}
so \(P(t) = 768,000 e^{0.062t}\text{.}\)
Checkpoint 5.82. Practice 8.
From 1994 to 1998, the number of personal computers connected to the Internet grew according to the formula
\begin{equation*}
N(t) = 2.8e^{0.85t}
\end{equation*}
where \(t = 0\) in 1994 and \(N\) is in millions. (Source: Los Angeles Times, September 6, 1999)
Evaluate \(N(1)\text{.}\) By what percent did the number of Internet users grow in one year?
Express the growth law in the form \(~N(t) = N_0 (1 + r)^t\text{.}\) (Hint: \(e^k = 1 + r\text{.}\))
Solution.
\(N(1)\approx 6.55\text{,}\) \(~134\%\)
\(\displaystyle N(t)\approx 2.8 (2.3396)^t \)
Now, what about exponential decay, where the the decay factor \(b\) is a number less than 1? If \(k\) is negative, then \(e^k\) is a number less than \(1\text{.}\) For example, if \(k = -2\text{,}\)
\begin{equation*}
e^{-2} = \frac{1}{e^2} \approx \frac{1}{7.3891} \approx 0.1353
\end{equation*}
Thus, for negative values of \(k\text{,}\) the function \(P(t) = P_0 e^{kt}\) describes exponential decay.
Exponential Growth and Decay.
The function
\begin{equation*}
\blert{P(t) = P_0 e^{kt}}
\end{equation*}
describes exponential growth if \(k \gt 0\text{,}\) and exponential decay if \(k \lt 0\text{.}\)
Checkpoint 5.83. QuickCheck 4.
The natural log of a number between 0 and 1 is
positive.
negative.
undefined.
between \(e^0\) and \(e^1\text{.}\)
Example 5.84.
Express the decay law \(N(t) = 60 (0.8)^t\) in the form \(N(t) = N_0 e^{kt}\text{.}\)
Solution.
For this decay law, \(N_0 = 60\) and \(b = 0.8\text{.}\) We would like to find a value for \(k\) so that \(e^k = b = 0.8\text{,}\) that is, we must solve the equation
\begin{equation*}
\begin{aligned}[t]
e^k \amp = 0.8\amp\amp \blert{\text{Take natural log of both sides.}}\\
\ln e^k\amp = \ln 0.8\amp\amp \blert{\text{Simplify.}}\\
k\amp = \ln 0.8 \approx -0.2231
\end{aligned}
\end{equation*}
Replacing \(b\) with \(e^k\text{,}\) we find that the decay law is
\begin{equation*}
N(t) \approx 60e^{-0.2231t}
\end{equation*}
Checkpoint 5.85. Practice 9.
A scientist isolates \(25\) grams of krypton-91, which decays according to the formula
\begin{equation*}
N(t) = 25e^{-0.07t}\text{,}
\end{equation*}
where \(t\) is in seconds.
-
Complete the table of values showing the amount of krypton-91 left at \(10\)-second intervals over the first minute.
| \(t\) |
\(0\) |
\(10\) |
\(20\) |
\(30\) |
\(40\) |
\(50\) |
\(60\) |
| \(N(t)\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
\(\hphantom{000}\) |
Use the table to choose a suitable window and graph the function \(N(t)\text{.}\)
-
Write and solve an equation to answer the question: How long does it take for 60% of the krypton-91 to decay?
Hint: If \(60\%\) of the krypton-91 has decayed, \(40\%\) of the original \(25\) grams remains.
Solution.
| \(t\) |
\(0\) |
\(10\) |
\(20\) |
\(30\) |
\(40\) |
\(50\) |
\(60\) |
| \(N(t)\) |
\(25\) |
\(12.41\) |
\(6.16\) |
\(3.06\) |
\(1.52\) |
\(0.75\) |
\(0.37\) |
\(25 e^{-0.07t} = 0.40(25)\text{;}\) \(~~t=\dfrac{\ln(0.4)}{-0.07}\approx 13.09 \) seconds
Checkpoint 5.86. Pause and Reflect.
Explain how to rewrite \(P(t)=P_0 b^t\) with the natural base.